Некоторые сведения из теории вероятности, использованные для решения задачи
парковки
Так как 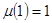 для
для 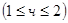 , то грубое приближение
, то грубое приближение 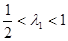 дает
дает
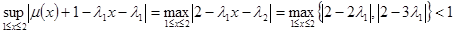 ,
,
следовательно по теореме 1 при условии 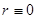 следует
следует
Теорема 3: существует постоянная 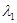
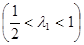 такая, что математическое ожидание
такая, что математическое ожидание 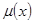 величины
величины 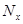 удовлетворяет соотношению
удовлетворяет соотношению
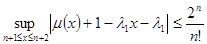 (
(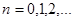 ) (2.2.13) [6]
) (2.2.13) [6]
Используя формулу Стирлинга 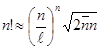 , получим
, получим
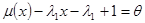
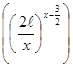 (2.2.14)
(2.2.14)
Определим 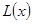 и
и 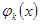 :
: 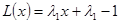
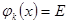
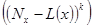 , где
, где 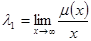
Из условия 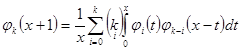 , при
, при 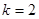 получаем
получаем
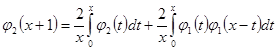 , (
, (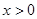 ) (2.2.15),
) (2.2.15),
учитывая, что 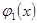 - левая часть выражения (2.2.14), следовательно
- левая часть выражения (2.2.14), следовательно
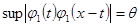
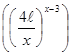 (2.2.15),
(2.2.15),
таким образом, 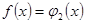 удовлетворяет
удовлетворяет 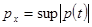 (
(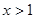 ),
),
где 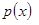 оценено формулой (2.2.15).
оценено формулой (2.2.15).
Из этих условии следует
Теорема 4: существует постоянная 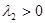 такая, что дисперсия
такая, что дисперсия 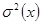 величины
величины 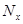 удовлетворяет соотношению
удовлетворяет соотношению 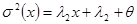
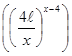 [6].
[6].
Рассмотрим соотношение: 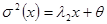
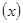 (2.2.16).
(2.2.16).
Докажем, что случайная величина 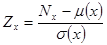 имеет асимптотически нормальное распределение с параметрами
имеет асимптотически нормальное распределение с параметрами 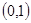 при
при 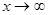 .
.
Для доказательства воспользуемся двумя леммами.
Лемма 1: пусть 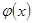 неотрицательная функция, определенная при
неотрицательная функция, определенная при 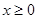 , ограниченная на конечных интервалах и удовлетворяющая соотношению
, ограниченная на конечных интервалах и удовлетворяющая соотношению 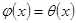 , тогда при
, тогда при 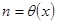 выполняется
выполняется 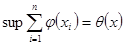 , где
, где 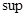 взят по всем наборам неотрицательных
взят по всем наборам неотрицательных 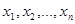 , при
, при 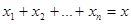 .
.
Лемма 2: рассмотрим 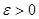
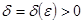 такое, что для всех
такое, что для всех 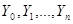 - независимых случайных величин, которые удовлетворяют
- независимых случайных величин, которые удовлетворяют
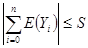
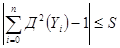

 (2.2.17)
(2.2.17)
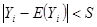
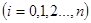
следует, что функция распределения 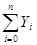 приближается равномерно по
приближается равномерно по 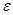 к нормальному распределению с нулевым математическим ожиданием и единичной дисперсией.
к нормальному распределению с нулевым математическим ожиданием и единичной дисперсией.
Перейти на страницу:
1 2 3 4

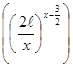 (2.2.14)
(2.2.14)
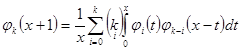 , при
, при 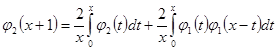 , (
, (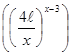 (2.2.15),
(2.2.15),
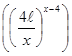 [6].
[6].