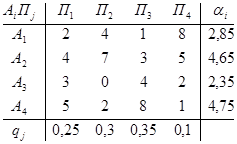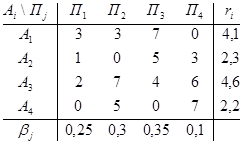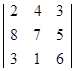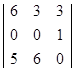Моделирование рисковых ситуаций
Задача 1 Определить верхнюю и нижнюю цену игры и, если это возможно, седловую точку. А = Решение: А = α = max min aij = 2 β = min max aij = 5 Так как α ≠ β, то седловой точки у этой матрицы нет. Ответ: у матрицы А седловой точки нет. Задача 2 Дана матрица выигрышей. Решить игру графически и аналитически. А = Решение: . Проверим наличие седловой точки: А = Так как α ≠ β, то седловая точка отсутствует. . Определим средние выигрыши А:
HA = (P,B1) = 4p + 5 (1- p)= (P,B2) = 6p + 2 (1- p) 3. Построим нижнюю огибающую на плоскости {р, Н}:
. Определим γ и р0. Точка (р0, γ) принадлежит обеим прямым H(P,B1) и H(P,B2). γ = 4 р0 + 5 (1- р0) γ = 6 р0 + 2 (1- р0) р0 - 3 (1- р0) = 0 р0 - 3 = 0 р0 = 3 р0 = 3/5 = 0,6 γ = 4 Ч 0,6 + 5 (1- 0,6) γ = 2,4 + 2 γ = 4,4 Решая эту систему, получим р0 = 0,6; γ = 4,4. Таким образом цена игры и оптимальная стратегия игрока А γ = 4,4; р0 = {0,6; 0,4}. Определим оптимальную стратегию Q0 = {q; 1 - q} игрока В:
γ = 4 q + 6 (1 - q) = 4,4 γ = 5 q + 2 (1 - q) = 4,4 Q0 = {0,8; 0,2} Ответ: р0 = {0,6; 0,4}, Q0 = {0,8; 0,2}, γ = 4,4. Задача 3 Дана матрица выигрышей и вероятностей qi состояний природы Пi. Определить оптимальные чистые стратегии в условиях неопределенности для матрицы выигрышей. А= Решение: . Матрица выигрышей А имеет вид: А= Определим средние выигрыши āi = ∑ āij qj для каждой стратегии А i: ā1 = 2Ч0,25 + 4Ч0,3 + 1Ч0,35 + 8Ч0,1 = 0,5 + 1,2 + 0,35 + 0,8 = 2,85; ā2 = 4Ч0,25 + 7Ч0,3 + 3Ч0,35 + 5Ч0,1 = 1 + 2,1 + 1,05 + 0,5 = 4,65; ā3 = 3Ч0,25 + 0Ч0,3 + 4Ч0,35 + 2Ч0,1 = 0,75 + 0 + 1,4 + 0,2 = 2,35; ā4 = 5Ч0,25 + 2Ч0,3 + 8Ч0,35 + 1Ч0,1 = 1,25 + 0,6 + 2,8 + 0,1 = 4,75. Согласно критерию оптимальности max∑ āij qj = 4,75. Следовательно, стратегия А 4 является оптимальной. . Матрица рисков R имеет вид: R = матрица выигрыш неопределенность стратегия Определим средние риски ri = ∑ rij qj для каждой стратегии А i: r1 = 3Ч0,25 + 3Ч0,3 + 7Ч0,35 + 0Ч0,1 = 0,75 + 0,9 + 2,45 + 0 = 4,1; r2 = 1Ч0,25 + 0Ч0,3 + 5Ч0,35 + 3Ч0,1 = 0,25 + 0 + 1,75 + 0,3 = 2,3; r3 = 2Ч0,25 + 7Ч0,3 + 4Ч0,35 + 6Ч0,1 = 0,5 + 2,1 + 1,4 + 0,6 = 4,6; r4 = 0Ч0,25 + 5Ч0,3 + 0Ч0,35 + 7Ч0,1 = 0 + 1,5 + 0 + 0,7 = 2,2. Согласно критерию min∑ rij qj= 2,2. Как следовала ожидать в силу эквивалентности стратегия А 4 является оптимальной. Ответ: стратегия А 4 является оптимальной. Задача 4 Используя критерии максимакса, Вальда, Сэвиджа и Гурвица (ж = 0,75) определить оптимальные чистые стратегии в условиях неопределенности для матрицы выигрышей. А= Решение: . Критерий максимакса: max max аi j = 8, следовательно, наилучшим решением будет А 2. . Максиминный критерий Вальда: W = max min аi j для А 1 min а1 j = 2 для А 2 min а2 j = 5 для А 3 min а3 j = 1 Следовательно, W = max min аi j= 5. таким образом, наилучший по критерию Вальда является стратегия А 2. . Критерий минимаксного риска Сэвиджа: S = min max rij R = для А 1 max r1j= 6 для А 2 max r2j= 1 для А 3 max r3j= 6 Следовательно, S = min max rij= 1, что соответствует стратегии А 2. . Критерии пессимизма - оптимизма Гурвица: HA = max (ж min аi j + (1 - ж) max аi j) Для матрицы выигрышей А критерий Гурвица имеет вид: для А 1 HA1 = 0,75Ч2 + (1 - 0,75)Ч4 = 1,5 + 0,25Ч4 = 1,5 + 1 = 2,5; для А 2 HA2 = 0,75Ч5 + (1 - 0,75)Ч8 = 3,75 + 0,25Ч8 = 3,75 + 2 = 5,75;
Перейти на страницу: 1 2
|

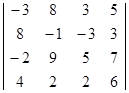
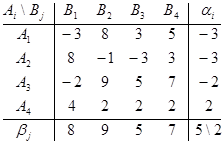
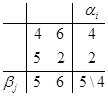

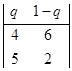
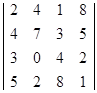 q1 = 0,25, q2 = 0,3, q3 = 0,35, q4 = 0,1
q1 = 0,25, q2 = 0,3, q3 = 0,35, q4 = 0,1