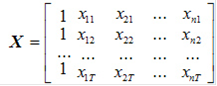Общие сведения о регрессионном анализе и методе наименьших квадратов

Метод наименьших квадратов - метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации расстояния между двумя векторами - вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.

Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных вследствие своей

простоты и

эффективности методов оценки параметров линейных эконометрических моделей.Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно «хорошо» отображать закономерности развития процесса .

Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2):

yt = a0 + a1 х1t + … + an хnt + εt.

Исходными данными при оценке параметров a0, a1,…, an является вектор значений зависимой переменной y

= (y1, y2,…, yT)' и матрица значений независимых переменных

в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели .

Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.

Регрессионный анализ - это статистический метод исследования зависимости случайной величины у от переменных (аргументов) хj (j = 1, 2,…, k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения xj.

Обычно предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием = φ(x1,…, хk), являющимся функцией от аргументов хj и с постоянной, не зависящей от аргументов дисперсией σ2.

Для проведения регрессионного анализа из (k + 1) - мерной генеральной совокупности (у, x1, х2,…, хj,…, хk) берется выборка объемом n, и каждое i-е наблюдение (объект) характеризуется значениями переменных (уi, xi1, хi2,…, хij,…, xik), где хij - значение j-й переменной для i-го наблюдения (i = 1, 2,…, n), уi - значение результативного признака для i-го наблюдения.

Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид

(6)

где βj - параметры регрессионной модели;

εj - случайные ошибки наблюдения, не зависимые друг от друга, имеют нулевую среднюю и дисперсию σ2.

Отметим, что модель (6) справедлива для всех i = 1,2,…, n, линейна относительно неизвестных параметров β0, β1,…, βj, …, βk и аргументов.

Как следует из (6), коэффициент регрессии Bj показывает, на какую величину в среднем изменится результативный признак у, если переменную хj увеличить на единицу измерения, т.е. является нормативным коэффициентом.

В матричной форме регрессионная модель имеет вид

(7)

где Y - случайный вектор-столбец размерности п х 1 наблюдаемых значений результативного признака (у1, у2,…. уn); Х - матрица размерности п х (k + 1) наблюдаемых значений аргументов, элемент матрицы х, рассматривается как неслучайная величина (i = 1, 2,…, n; j=0,1,…,

k; x0i, = 1); β - вектор-столбец размерности (k + 1) х 1 неизвестных, подлежащих оценке параметров модели (коэффициентов регрессии); ε - случайный вектор-столбец размерности п х 1 ошибок наблюдений (остатков). Компоненты вектора εi не зависимы друг от друга, имеют нормальный закон распределения с нулевым математическим ожиданием (M