Пример решения транспортной задачи методом потенциалов

u2=0

v1=2-u2=2-0=2;

v2=3-u2=3-0=3;

v3=4-u2=4-0=4;

u1=1-v1=1-2=-1;

u3=7-v3=7-4=3;

v4=12-u3=12-3=9;

u4=0-v4=0-9=-9.

Значения потенциалов записываем рядом с запасами или запросами соответствующих поставщиков и потребителей в таблицу (табл. 6.15).

Система уравнений для нахождения потенциалов достаточно проста, обычно ее решают устно, глядя на таблицу задачи, ее занятые клетки и известные потенциалы. Любой неизвестный потенциал, соответствующий занятой клетке, равен находящейся в этой клетке стоимости, минус известный потенциал, соответствующий этой клетке (6.14), (6.15).

Таблица 6.15

4. Проверяем опорное решение X1 на оптимальность. С этой целью вычисляем оценки для всех незаполненных клеток таблицы (для всех занятых ).

Положительные оценки записывают в левые нижние углы соответствующих клеток таблицы, вместо отрицательных просто ставим знак “-”.

Начальное опорное решение не является оптимальным, так как имеются положительные оценки.

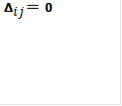
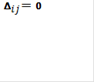. Переходим к новому опорному решению. Находим клетку таблицы, которой соответствует наибольшая положительная оценка. Имеем для клетки (1,4). Для этой клетки строим цикл. Ставим в нее знак “+”, присоединяем ее к занятым клеткам и применяем метод вычеркивания. После проведения вычеркиваний в таблице остаются только образующие цикл клетки. Цикл изображен в табл. 6.15. на основании теоремы 6.6 такой цикл единственный . В угловых точках цикла расставляются поочередно знаки “+” и “”, начиная с “+” в клетке (1,4). В клетки, отмеченные знаком “+” добавляется груз θ, а из клеток, отмеченных знаком минус, вычитается такой же по величине груз. Определяем величину груза θ, перераспределяемого по циклу. Она равняется значению наименьшей из перевозок в клетках цикла, отмеченных знаком “-”