Применение графического метода и симплекс-метода для решения задач линейного программирования
3. Имеются три пункта поставки однородного груза - А1; А2; А3 и пять пунктов потребления этого груза - В1; В2; В3; В4; В5. В пунктах А1; А2; А3 находится 200; 450; 250 единиц груза соответственно, который надо доставить в пункты В1; В2; В3; В4; В5 в количестве 100; 125; 325; 250; 100 соответственно. Расстояние между пунктами задано в километрах следующей матрицей:
Требуется найти оптимальный план закрепления потребителей за поставщиками однородного груза при условии минимизации общего пробега автомобилей. Рассмотреть два метода получения начального плана. 1. Графический метод решения задачи линейного программирования
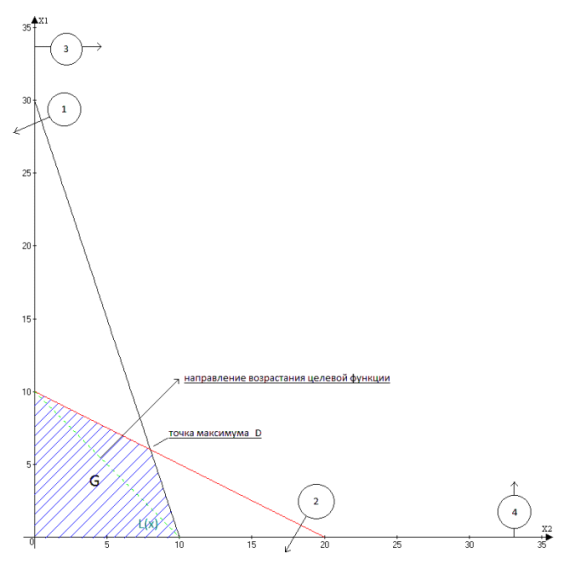
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат. Из условий ограничения получим область допустимых значений G
Рисунок 1. Графический метод решения задачи линейного программирования. Направление возрастания целевой функции указано на рисунке 1. Соответственно, точкой максимума является точка D. Найдем ее координаты исходя из того, что она является точкой пересечения графиков (1) и (2). Для этого решим систему уравнений:
Решением этой системы уравнений будут координаты точки D: x1 = 6, x2 = 8. Подставляя эти значения в целевую функцию, получим окончательный ответ: . Решение задачи линейного программирования симплекс-методом
Запишем задачу в канонической форме как того требует симплекс-метод, для этого введем две переменные y4 и y5, получим:
В получившейся системе отсутствуют базисные переменные, поэтому в первое и второе уравнения добавляем искусственные переменные y6 и y7. Чтобы можно было применить симплекс-метод система уравнений-ограничений должна быть системой с базисом, т.е. в каждом уравнении должна быть переменная с коэффициентом 1, которая входит только в одно уравнение системы, в нашем случае это y6 и y7. Получаем, так называемую, М-задачу:
Данная система является системой с базисом, следовательно, для решения можно применить симплекс-метод. Запишем начальную симплекс-таблицу:
|

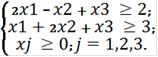

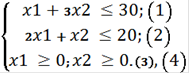
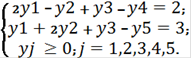
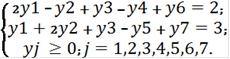 = (0, 0, 0, 0, 0, 2, 3)T
= (0, 0, 0, 0, 0, 2, 3)T