Проверка гипотезы о распределении случайной величины по
показательному закону
Количество интервалов - 8
Количество параметров распределения - 1
Уровень значимости - 0,05
Число степеней свободы - 6
Таблица 5 - Эмпирическое распределение время между инцидентами | |
начало интервала |
конец интервала |
частота |
частость |
середина интервала |
отклонение от среднего | |
№ |
Xi |
Xi+1 |
Mi |
Wi |
Xi¯ |
Xi-Xв | |
1 |
0,05 |
1,41 |
52 |
0,52 |
0,73 |
-1,98 | |
2 |
1,41 |
2,78 |
26 |
0,26 |
2,10 |
-0,61 | |
3 |
2,78 |
4,14 |
10 |
0,1 |
3,46 |
0,75 | |
4 |
4,14 |
5,51 |
7 |
0,07 |
4,83 |
2,12 | |
5 |
5,51 |
6,87 |
0 |
0 |
6,19 |
3,48 | |
6 |
6,87 |
8,24 |
3 |
0,03 |
7,56 |
4,85 | |
7 |
8,24 |
9,60 |
1 |
0,01 |
8,92 |
6,21 | |
8 |
9,60 |
10,97 |
1 |
0,01 |
10,29 |
7,58 | |
Итого: |
- |
- |
100 |
1 |
- |
- |
Построим гистограмму эмпирического распределения время между инцидентами (рис. 3):
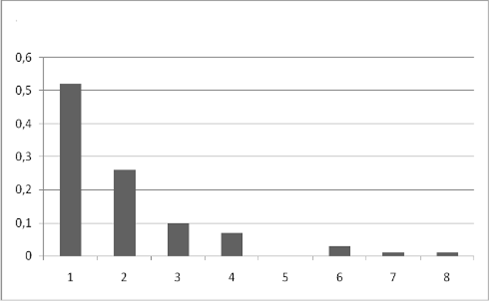
Рис. 3
Вычисление теоретических вероятностейпопадания в заданный интервал экспоненциально распределенной случайной величины (таблица 5):
Таблица 5 | | | | |
вероятность |
теоретические частоты | | |
-л*Xi |
-л*Xi+1 |
e^(-л*Xi) |
e^(-л*Xi+1) |
Pi |
Mi' |
(Mi-Mi')² |
(Mi-Mi')²/Mi' | |
-0,025 |
-0,697 |
0,976 |
0,498 |
0,478 |
47,784 |
17,777 |
0,372 | |
-0,697 |
-1,370 |
0,498 |
0,254 |
0,244 |
24,384 |
2,611 |
0,107 | |
-1,370 |
-2,043 |
0,254 |
0,130 |
0,124 |
12,443 |
5,970 |
0,480 | |
-2,043 |
-2,716 |
0,130 |
0,066 |
0,063 |
6,350 |
0,423 |
0,067 | |
-2,716 |
-3,388 |
0,066 |
0,034 |
0,032 |
3,240 |
10,500 |
3,240 | |
-3,388 |
-4,061 |
0,034 |
0,017 |
0,017 |
1,654 |
1,813 |
1,096 | |
-4,061 |
-4,734 |
0,017 |
0,009 |
0,008 |
0,844 |
0,024 |
0,029 | |
-4,734 |
-5,407 |
0,009 |
0,004 |
0,004 |
0,431 |
0,324 |
0,753 | |
- |
- |
- |
- |
1 |
- |
- |
6,14 |
|